题目出处
题目描述

个人解法
思路:
假设整数为a,转换为字符串b
如果b.length=num为奇数,判断b[0]==b[num-1],b[1]==b[num-2]…b[num/2-1]==b[num/2+1],如果上述表达式全为true,则是回文数
如果b.length=num为偶数,判断b[0]==b[num-1],b[1]==b[num-2]…b[num/2-1]==b[num/2],如果上述表达式全为true,则是回文数
代码示例:(Java)
public boolean isPalindrome(int x) {
String str = Integer.valueOf(x).toString();
int length = str.length();
int matchSize = length / 2;
int j = 0;
for (int i = 0; i < length / 2; i++) {
boolean match = str.charAt(i) == str.charAt(length - 1 - i);
if (match) {
j++;
}
}
return j == matchSize;
}
复杂度分析
o(n)
官方解法
方法1:反转一半数字
思路:


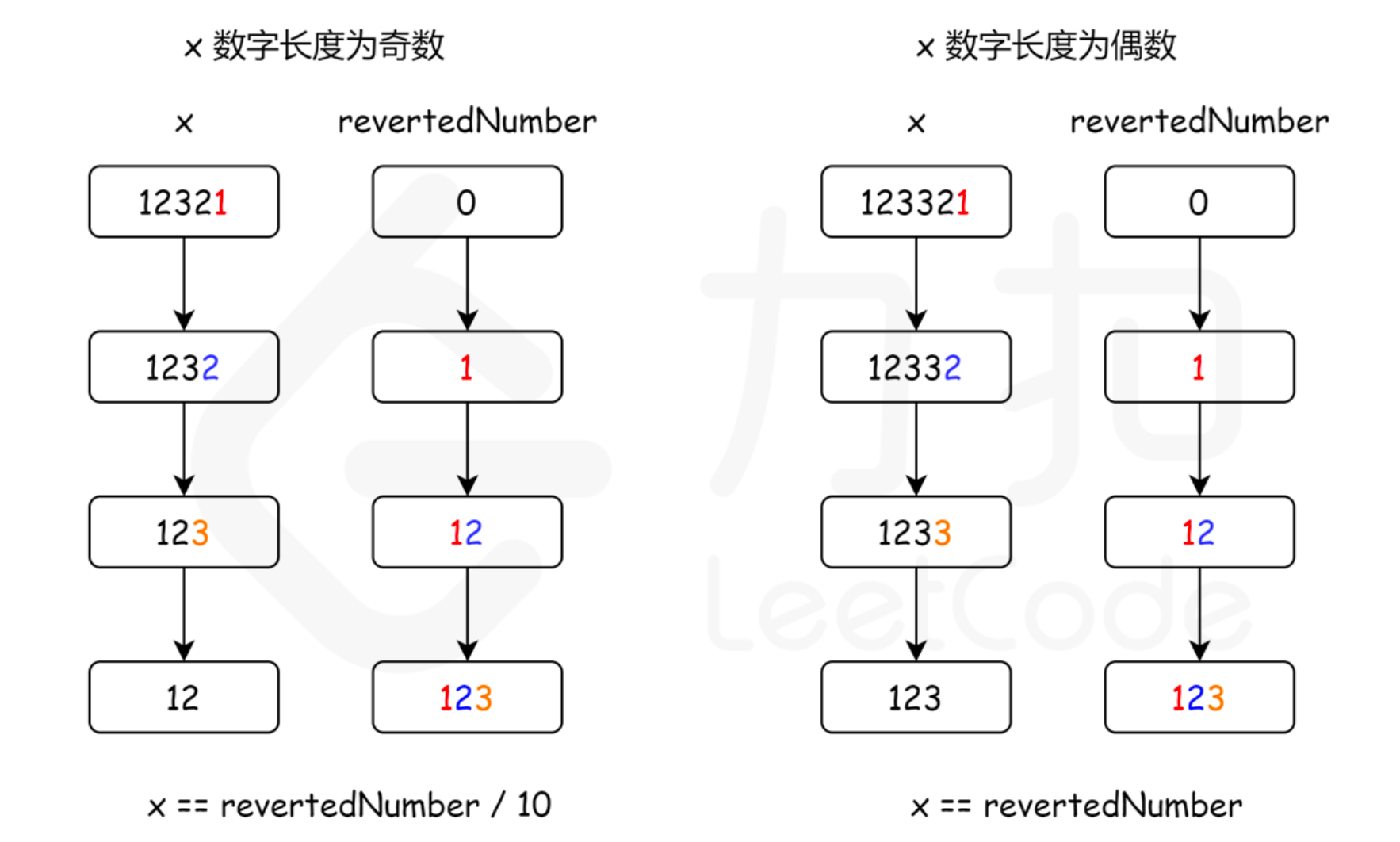
代码示例:(Java)
public boolean isPalindrome(int x) {
// 特殊情况:
// 如上所述,当 x < 0 时,x 不是回文数。
// 同样地,如果数字的最后一位是 0,为了使该数字为回文,
// 则其第一位数字也应该是 0
// 只有 0 满足这一属性
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int revertedNumber = 0;
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
// 当数字长度为奇数时,我们可以通过 revertedNumber/10 去除处于中位的数字。
// 例如,当输入为 12321 时,在 while 循环的末尾我们可以得到 x = 12,revertedNumber = 123,
// 由于处于中位的数字不影响回文(它总是与自己相等),所以我们可以简单地将其去除。
return x == revertedNumber || x == revertedNumber / 10;
}
复杂度分析

考察知识点
1.回文数
回文数

