题目出处
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
前言

方法1:基于集合的回溯
思路:

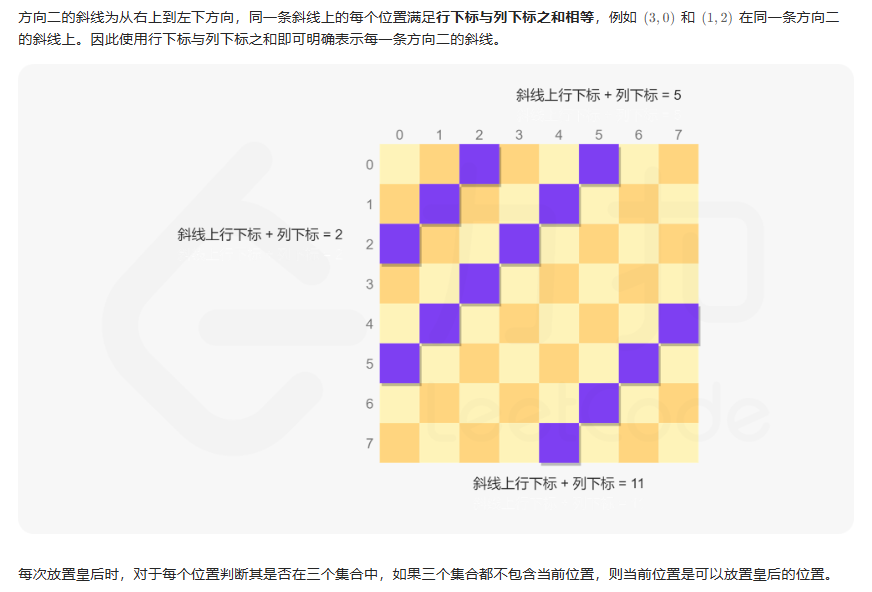
代码示例:(Java)
public class Solution1 {
public List<List<String>> solveNQueens(int n) {
List<List<String>> solutions = new ArrayList<List<String>>();
int[] queens = new int[n];
Arrays.fill(queens, -1);
Set<Integer> columns = new HashSet<Integer>();
Set<Integer> diagonals1 = new HashSet<Integer>();
Set<Integer> diagonals2 = new HashSet<Integer>();
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
public void backtrack(List<List<String>> solutions, int[] queens, int n, int row, Set<Integer> columns, Set<Integer> diagonals1, Set<Integer> diagonals2) {
if (row == n) {
List<String> board = generateBoard(queens, n);
solutions.add(board);
} else {
for (int i = 0; i < n; i++) {
if (columns.contains(i)) {
continue;
}
int diagonal1 = row - i;
if (diagonals1.contains(diagonal1)) {
continue;
}
int diagonal2 = row + i;
if (diagonals2.contains(diagonal2)) {
continue;
}
queens[row] = i;
columns.add(i);
diagonals1.add(diagonal1);
diagonals2.add(diagonal2);
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
queens[row] = -1;
columns.remove(i);
diagonals1.remove(diagonal1);
diagonals2.remove(diagonal2);
}
}
}
public List<String> generateBoard(int[] queens, int n) {
List<String> board = new ArrayList<String>();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}
}
复杂度分析

方法2:基于位运算的回溯
思路:

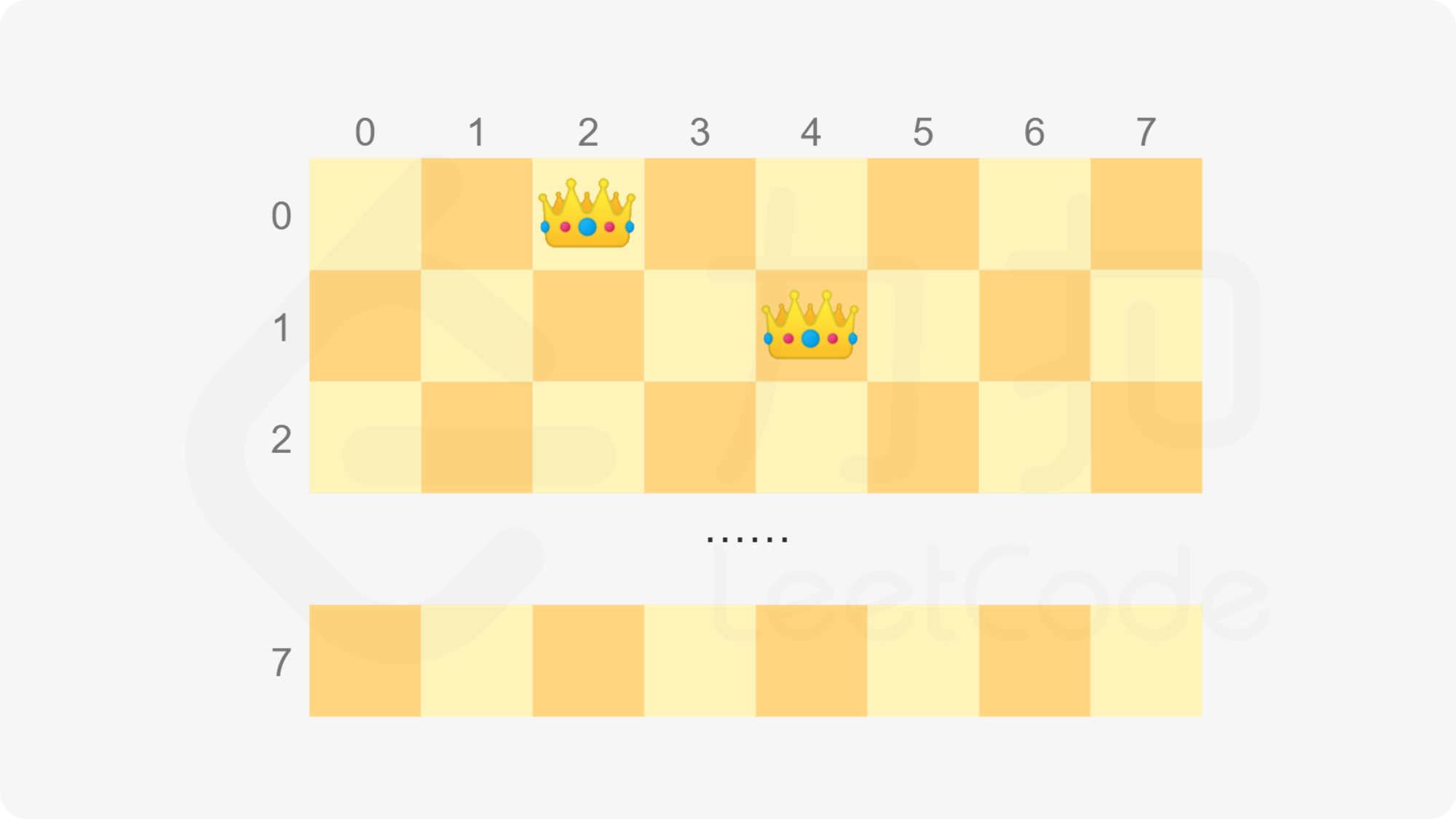

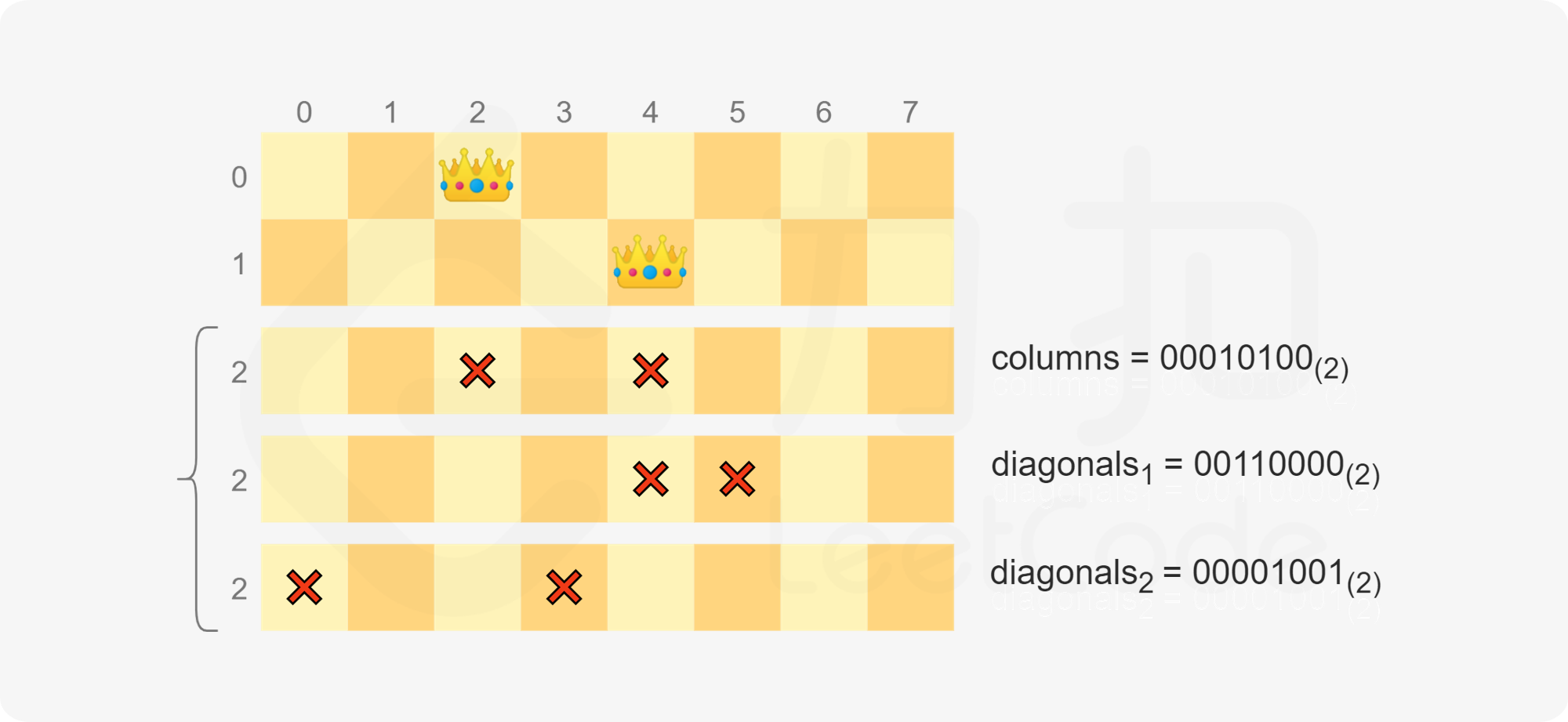



代码示例:(Java)
public class Solution2 {
public List<List<String>> solveNQueens(int n) {
int[] queens = new int[n];
Arrays.fill(queens, -1);
List<List<String>> solutions = new ArrayList<List<String>>();
solve(solutions, queens, n, 0, 0, 0, 0);
return solutions;
}
public void solve(List<List<String>> solutions, int[] queens, int n, int row, int columns, int diagonals1, int diagonals2) {
if (row == n) {
List<String> board = generateBoard(queens, n);
solutions.add(board);
} else {
int availablePositions = ((1 << n) - 1) & (~(columns | diagonals1 | diagonals2));
while (availablePositions != 0) {
int position = availablePositions & (-availablePositions);
availablePositions = availablePositions & (availablePositions - 1);
int column = Integer.bitCount(position - 1);
queens[row] = column;
solve(solutions, queens, n, row + 1, columns | position, (diagonals1 | position) << 1, (diagonals2 | position) >> 1);
queens[row] = -1;
}
}
}
public List<String> generateBoard(int[] queens, int n) {
List<String> board = new ArrayList<String>();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}
}
复杂度分析

小结

考察知识点
1.位运算

