题目出处
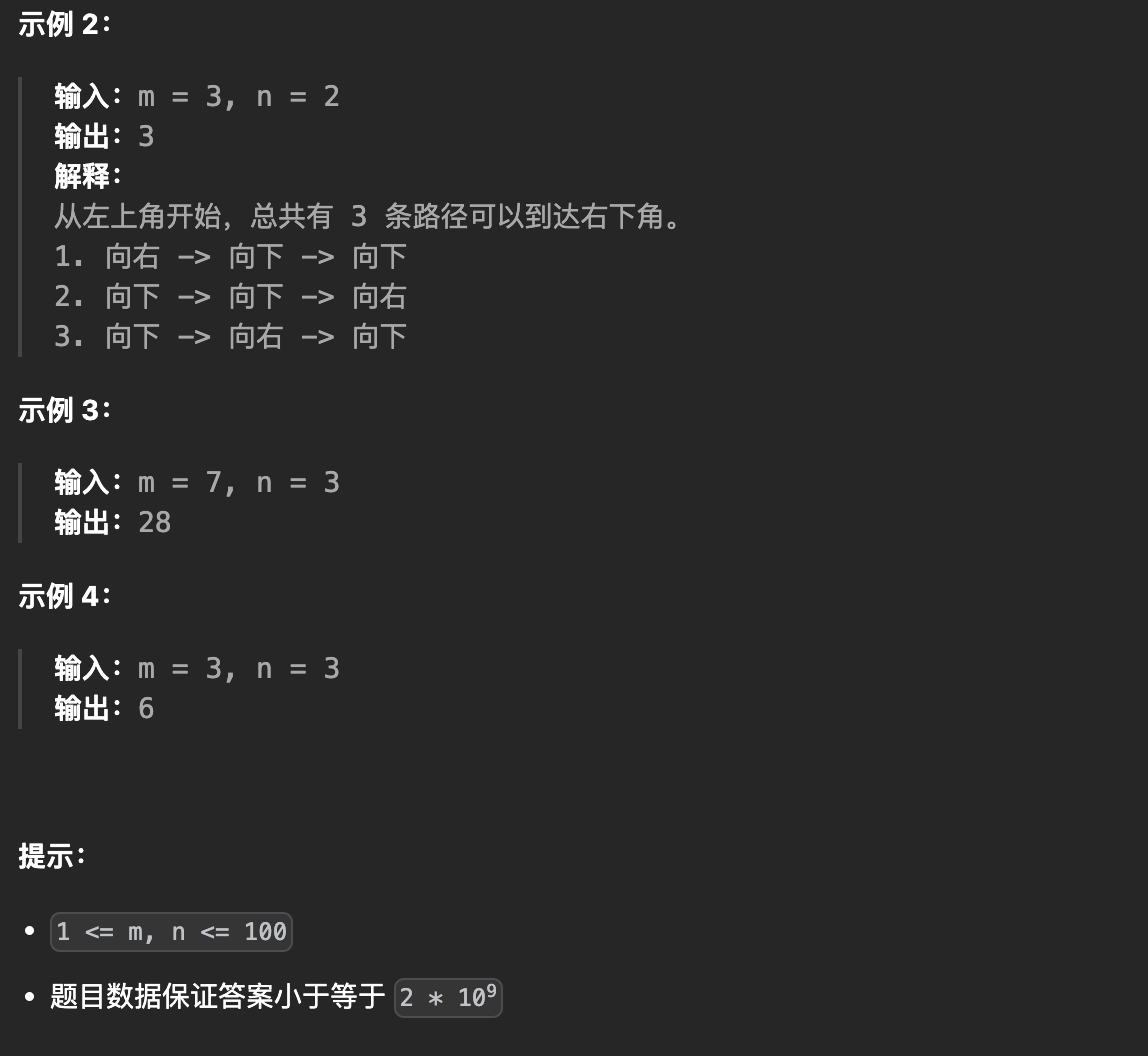
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
方法1:动态规划
思路:

代码示例:(Java)
public class Solution1 {
public int uniquePaths(int m, int n) {
int[][] f = new int[m][n];
for (int i = 0; i < m; ++i) {
f[i][0] = 1;
}
for (int j = 0; j < n; ++j) {
f[0][j] = 1;
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
return f[m - 1][n - 1];
}
}
此外,由于 f(i,j) 仅与第 i 行和第 i−1 行的状态有关,因此我们可以使用滚动数组代替代码中的二维数组,使空间复杂度降低为 O(n)。
public class Solution2 {
public int uniquePaths(int m, int n) {
int[] f = new int[n];
for (int i = 0; i < n; ++i) {
f[i] = 1;
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
f[j] += f[j - 1];
}
}
return f[n - 1];
}
}
复杂度分析

方法2:组合数学
思路:

代码示例:(Java)
public class Solution3 {
public int uniquePaths(int m, int n) {
long ans = 1;
for (int x = n, y = 1; y < m; ++x, ++y) {
ans = ans * x / y;
}
return (int) ans;
}
}
复杂度分析


