题目出处
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
想法
编辑距离算法被数据科学家广泛应用,是用作机器翻译和语音识别评价标准的基本算法。
最直观的方法是暴力检查所有可能的编辑方法,取最短的一个。所有可能的编辑方法达到指数级,但我们不需要进行这么多计算,因为我们只需要找到距离最短的序列而不是所有可能的序列。
方法1:动态规划
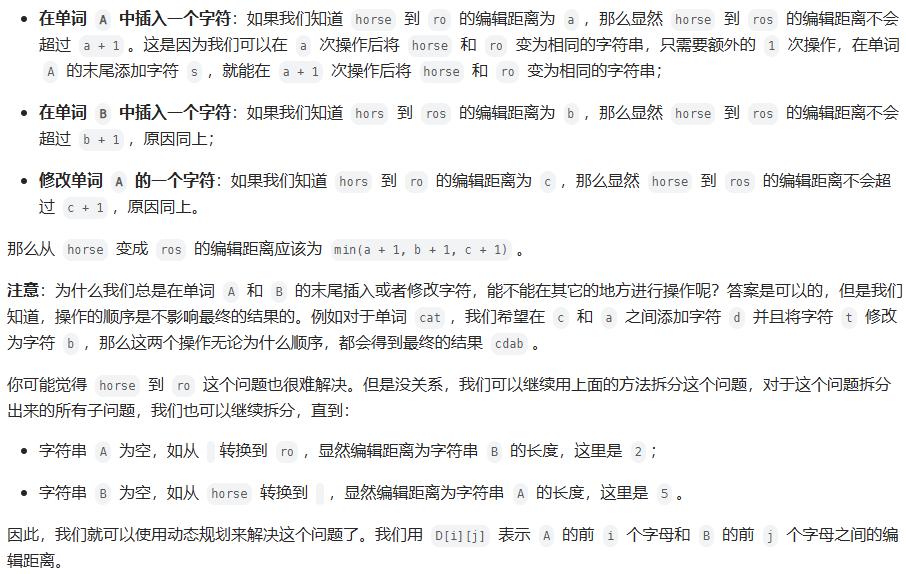
思路:





代码示例:(Java)
public class Solution1 {
public int minDistance(String word1, String word2) {
int n = word1.length();
int m = word2.length();
// 有一个字符串为空串
if (n * m == 0) {
return n + m;
}
// DP 数组
int[][] D = new int[n + 1][m + 1];
// 边界状态初始化
for (int i = 0; i < n + 1; i++) {
D[i][0] = i;
}
for (int j = 0; j < m + 1; j++) {
D[0][j] = j;
}
// 计算所有 DP 值
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < m + 1; j++) {
int left = D[i - 1][j] + 1;
int down = D[i][j - 1] + 1;
int left_down = D[i - 1][j - 1];
if (word1.charAt(i - 1) != word2.charAt(j - 1)) {
left_down += 1;
}
D[i][j] = Math.min(left, Math.min(down, left_down));
}
}
return D[n][m];
}
}
复杂度分析
- 时间复杂度 :O(mn),其中 m 为 word1 的长度,n 为 word2 的长度。
- 空间复杂度 :O(mn),我们需要大小为 O(mn) 的 D 数组来记录状态值。

