题目出处
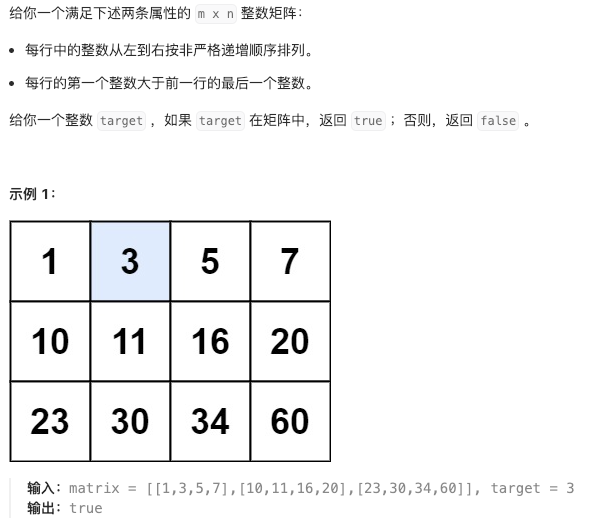
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
方法1:两次二分查找
思路:

代码示例:(Java)
public class Solution1 {
public boolean searchMatrix(int[][] matrix, int target) {
int rowIndex = binarySearchFirstColumn(matrix, target);
if (rowIndex < 0) {
return false;
}
return binarySearchRow(matrix[rowIndex], target);
}
public int binarySearchFirstColumn(int[][] matrix, int target) {
int low = -1, high = matrix.length - 1;
while (low < high) {
int mid = (high - low + 1) / 2 + low;
if (matrix[mid][0] <= target) {
low = mid;
} else {
high = mid - 1;
}
}
return low;
}
public boolean binarySearchRow(int[] row, int target) {
int low = 0, high = row.length - 1;
while (low <= high) {
int mid = (high - low) / 2 + low;
if (row[mid] == target) {
return true;
} else if (row[mid] > target) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return false;
}
}
复杂度分析

方法2:一次二分查找
思路:

代码示例:(Java)
public class Solution2 {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
int low = 0, high = m * n - 1;
while (low <= high) {
int mid = (high - low) / 2 + low;
int x = matrix[mid / n][mid % n];
if (x < target) {
low = mid + 1;
} else if (x > target) {
high = mid - 1;
} else {
return true;
}
}
return false;
}
}
复杂度分析

结语
两种方法殊途同归,都利用了二分查找,在二维矩阵上寻找目标值。值得注意的是,若二维数组中的一维数组的元素个数不一,方法二将会失效,而方法一则能正确处理。

