题目出处
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
方法1:递归实现组合型枚举
思路:
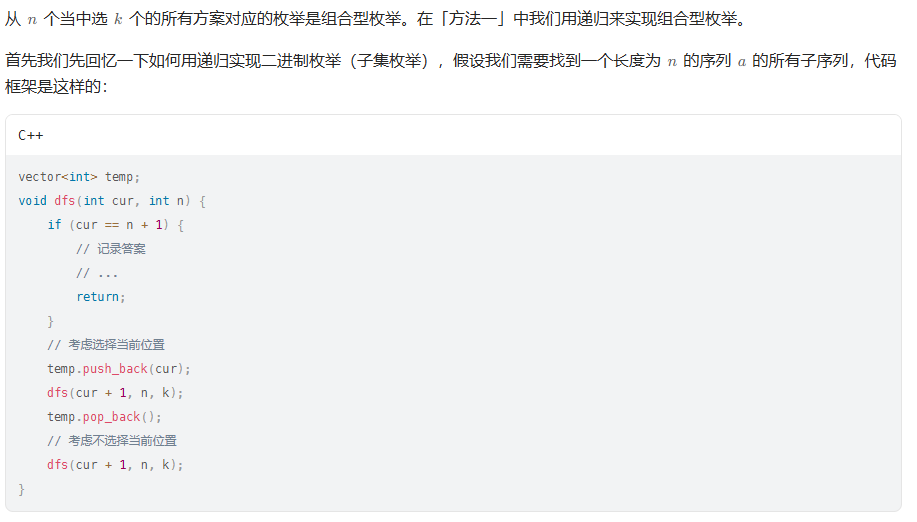
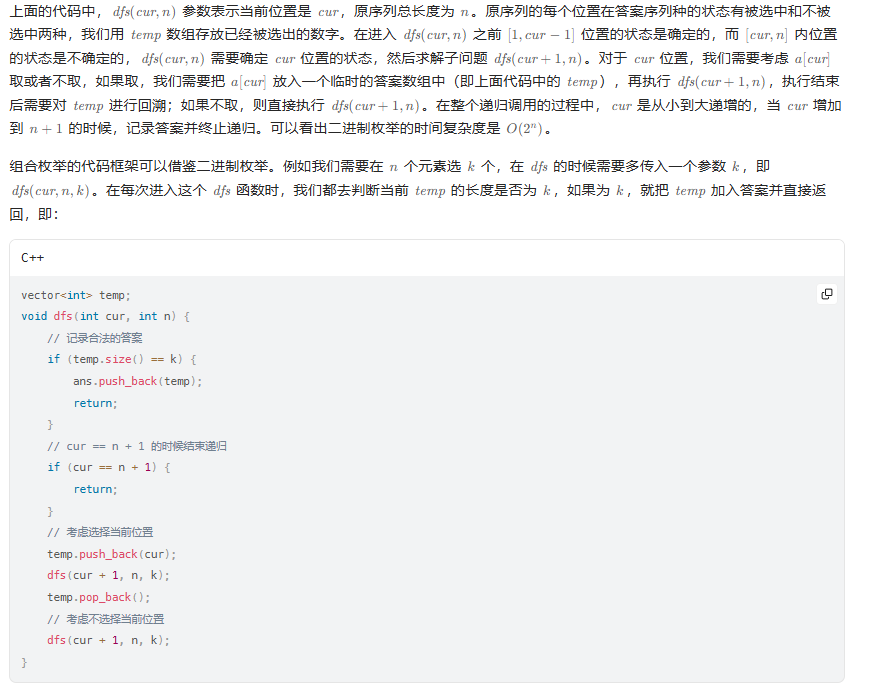
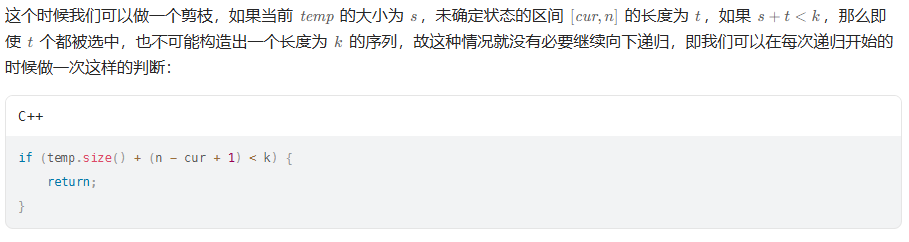
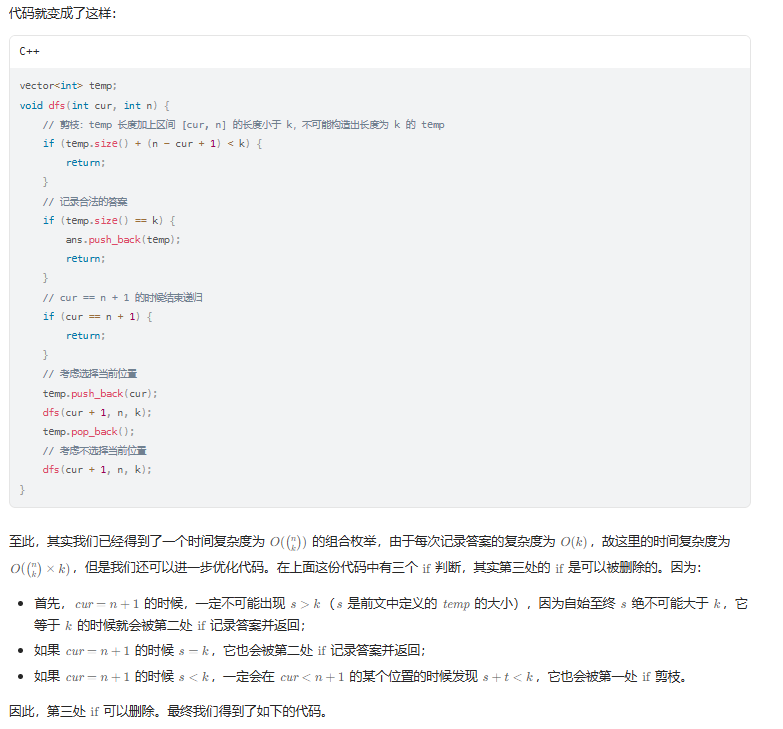
代码示例:(Java)
public class Solution1 {
List<Integer> temp = new ArrayList<Integer>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
public List<List<Integer>> combine(int n, int k) {
dfs(1, n, k);
return ans;
}
public void dfs(int cur, int n, int k) {
// 剪枝:temp 长度加上区间 [cur, n] 的长度小于 k,不可能构造出长度为 k 的 temp
if (temp.size() + (n - cur + 1) < k) {
return;
}
// 记录合法的答案
if (temp.size() == k) {
ans.add(new ArrayList<Integer>(temp));
return;
}
// 考虑选择当前位置
temp.add(cur);
dfs(cur + 1, n, k);
temp.remove(temp.size() - 1);
// 考虑不选择当前位置
dfs(cur + 1, n, k);
}
}
复杂度分析

方法2:非递归(字典序法)实现组合型枚举
思路:
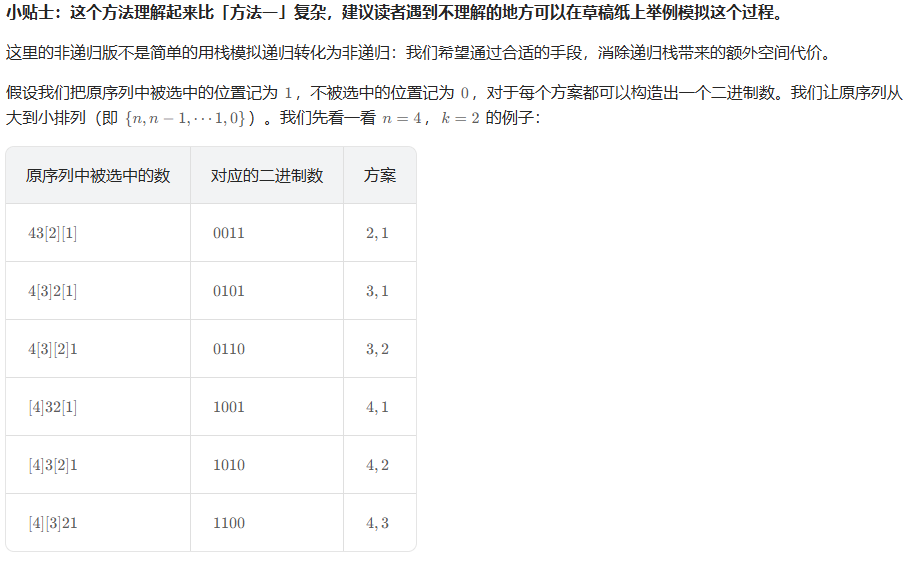

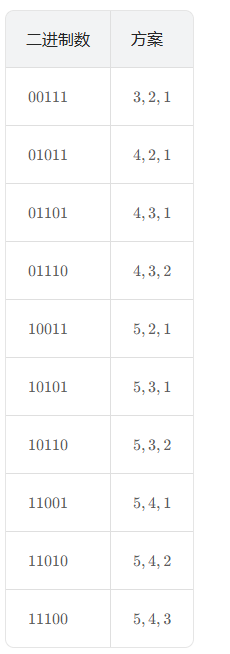

代码示例:(Java)
public class Solution2 {
List<Integer> temp = new ArrayList<Integer>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
public List<List<Integer>> combine(int n, int k) {
List<Integer> temp = new ArrayList<Integer>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
// 初始化
// 将 temp 中 [0, k - 1] 每个位置 i 设置为 i + 1,即 [0, k - 1] 存 [1, k]
// 末尾加一位 n + 1 作为哨兵
for (int i = 1; i <= k; ++i) {
temp.add(i);
}
temp.add(n + 1);
int j = 0;
while (j < k) {
ans.add(new ArrayList<Integer>(temp.subList(0, k)));
j = 0;
// 寻找第一个 temp[j] + 1 != temp[j + 1] 的位置 t
// 我们需要把 [0, t - 1] 区间内的每个位置重置成 [1, t]
while (j < k && temp.get(j) + 1 == temp.get(j + 1)) {
temp.set(j, j + 1);
++j;
}
// j 是第一个 temp[j] + 1 != temp[j + 1] 的位置
temp.set(j, temp.get(j) + 1);
}
return ans;
}
}
复杂度分析


