题目出处
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
方法1:动态规划
思路:

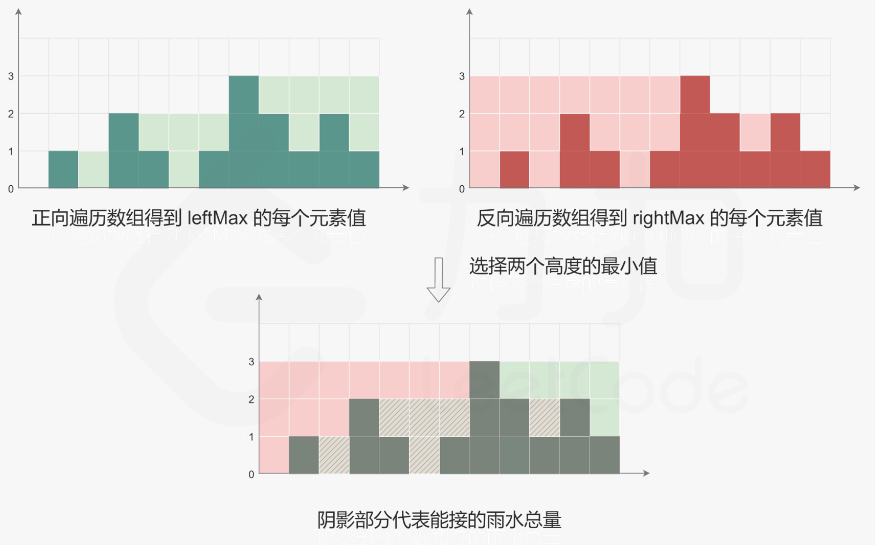
代码示例:(Java)
public class Solution1 {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int[] leftMax = new int[n];
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
int[] rightMax = new int[n];
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(n),其中 n 是数组 height 的长度。计算数组 leftMax 和 rightMax 的元素值各需要遍历数组 height 一次,计算能接的雨水总量还需要遍历一次。
- 空间复杂度:O(n),其中 n 是数组 height 的长度。需要创建两个长度为 n 的数组 leftMax 和 rightMax。
方法2:单调栈
思路:

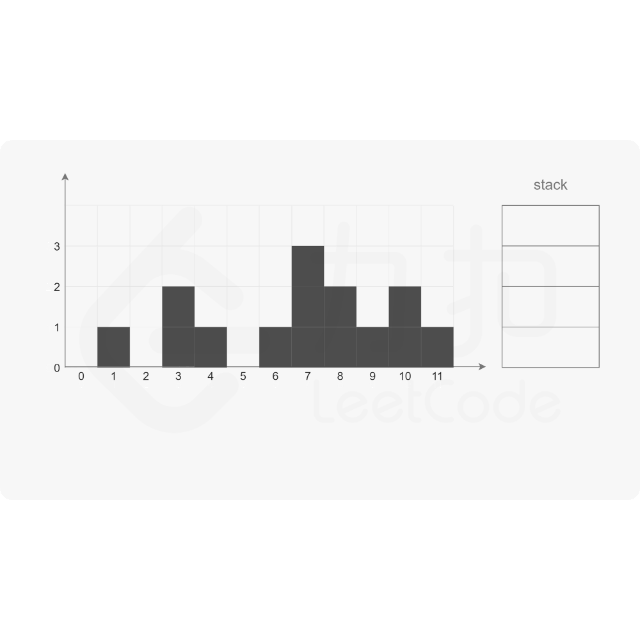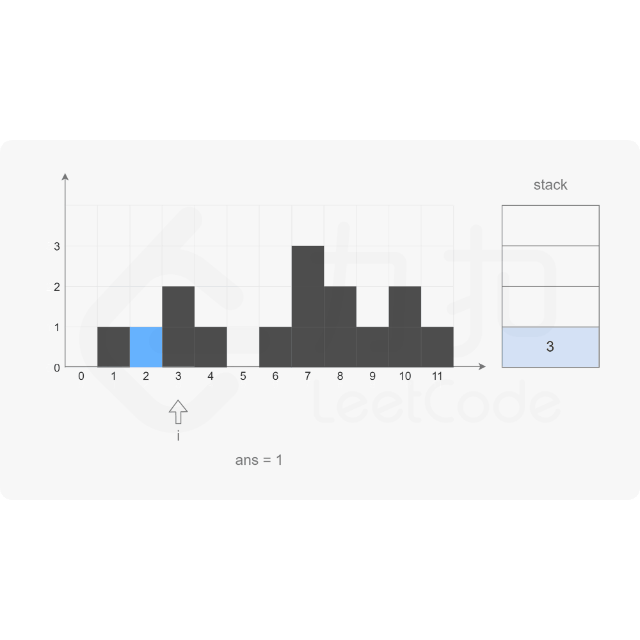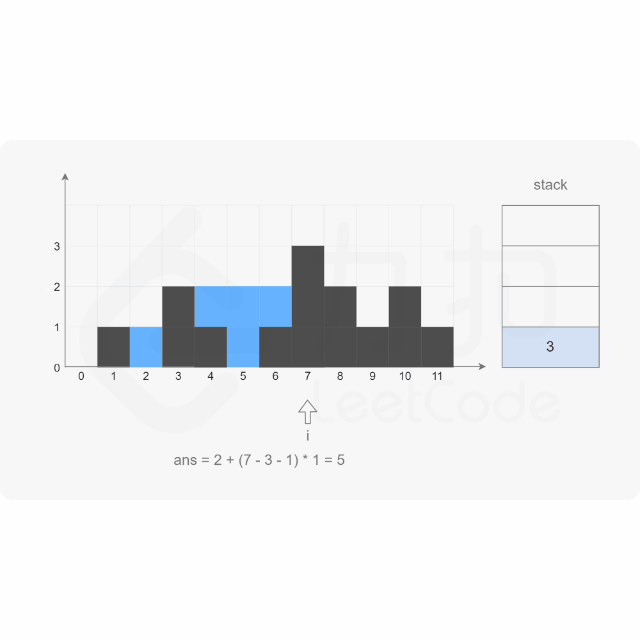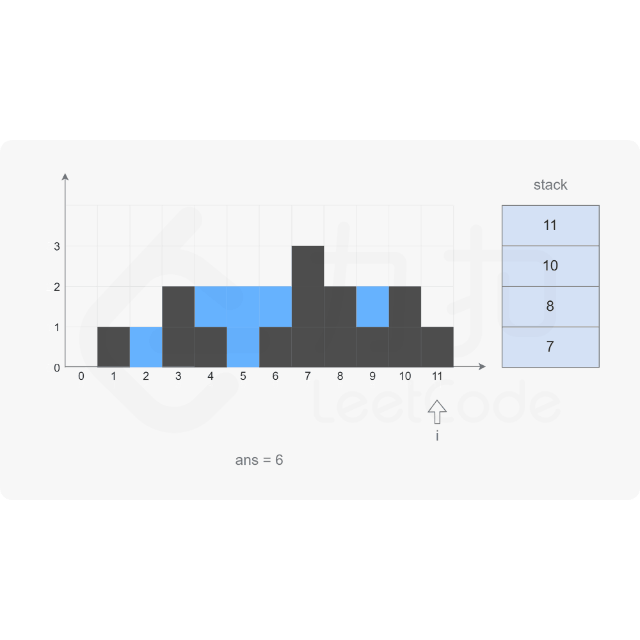
代码示例:(Java)
public class Solution2 {
public int trap(int[] height) {
int ans = 0;
Deque<Integer> stack = new LinkedList<Integer>();
int n = height.length;
for (int i = 0; i < n; ++i) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop();
if (stack.isEmpty()) {
break;
}
int left = stack.peek();
int currWidth = i - left - 1;
int currHeight = Math.min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stack.push(i);
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(n),其中 n 是数组 height 的长度。从 0 到 n−1 的每个下标最多只会入栈和出栈各一次。
- 空间复杂度:O(n),其中 n 是数组 height 的长度。空间复杂度主要取决于栈空间,栈的大小不会超过 n。
方法3:双指针
思路:

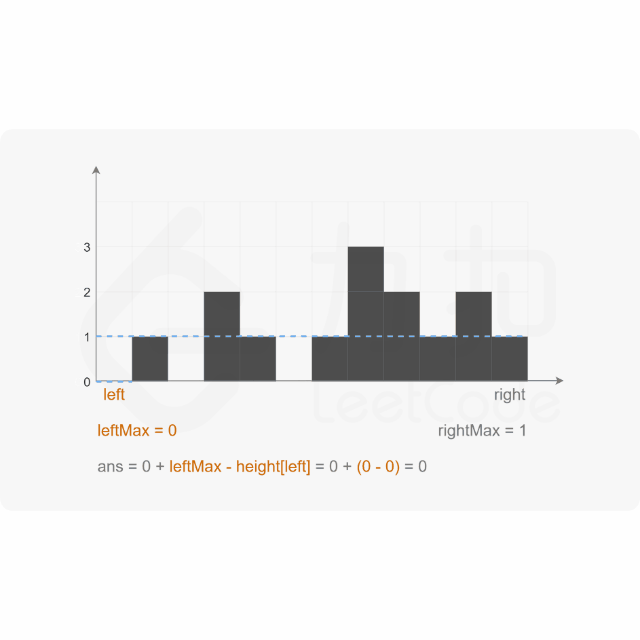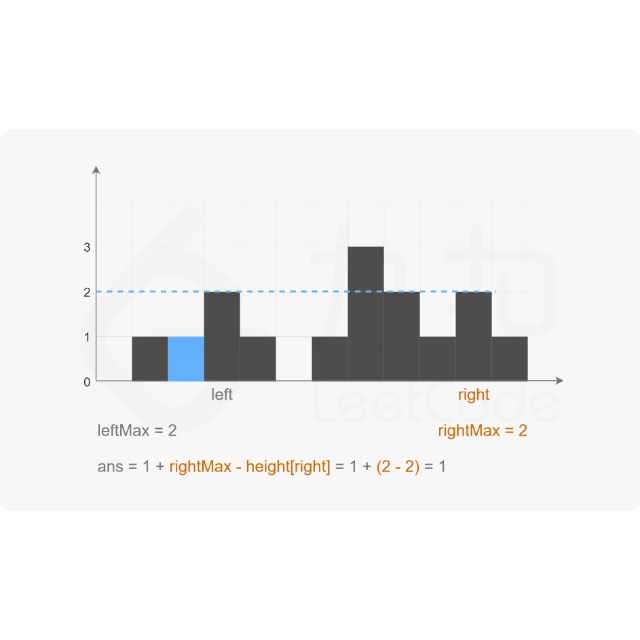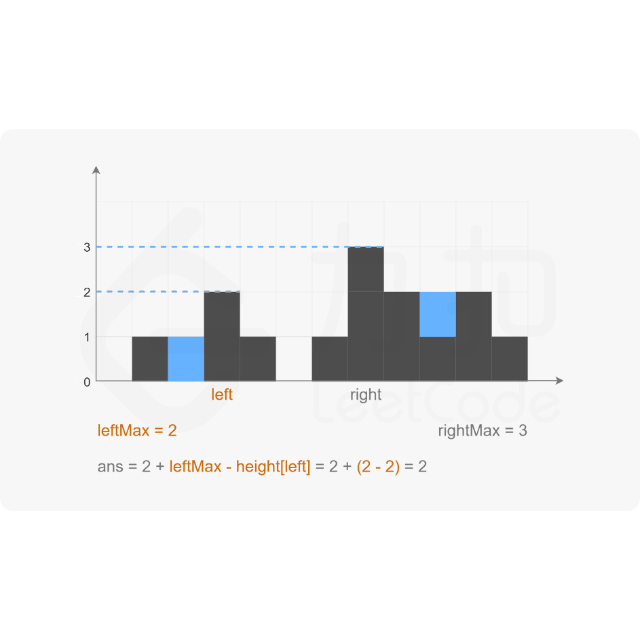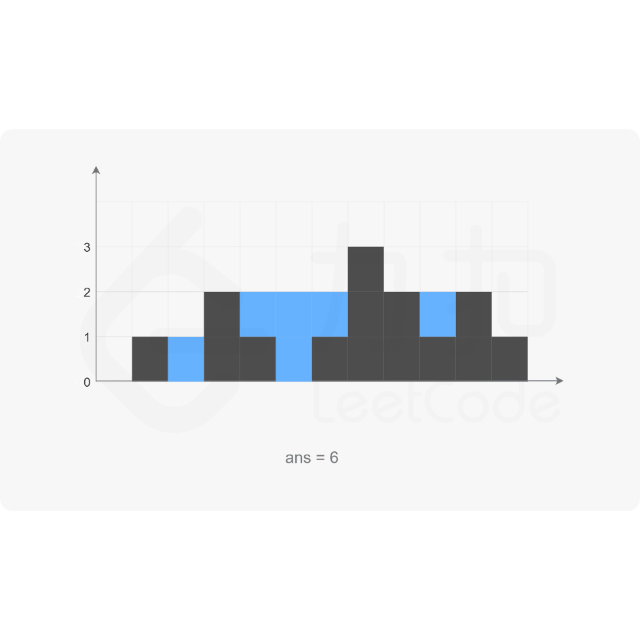
代码示例:(Java)
public class Solution3 {
public int trap(int[] height) {
int ans = 0;
int left = 0, right = height.length - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(n),其中 n 是数组 height 的长度。两个指针的移动总次数不超过 n。
- 空间复杂度:O(1)。只需要使用常数的额外空间。
考察知识点
1.Deque
收获
1.gitee源码用相对路径在gitee可以跳转,在外部网站不可以,因此源码地址改为了绝对路径

