题目出处
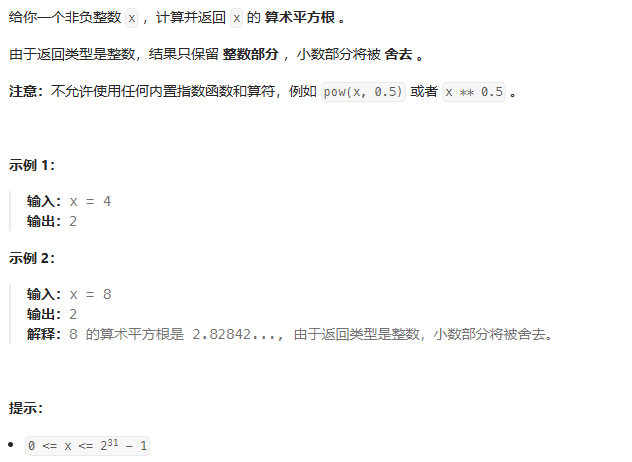
题目描述
个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
前言

方法1:袖珍计算器算法
思路:

代码示例:(Java)
public class Solution1 {
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = (int) Math.exp(0.5 * Math.log(x));
return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
}
}
复杂度分析
- 时间复杂度:O(1),由于内置的 exp 函数与 log 函数一般都很快,我们在这里将其复杂度视为 O(1)。
- 空间复杂度:O(1)。
方法2:二分查找
思路:

代码示例:(Java)
public class Solution2 {
public int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long) mid * mid <= x) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(logx),即为二分查找需要的次数。
- 空间复杂度:O(1)。
方法3:牛顿迭代
思路:

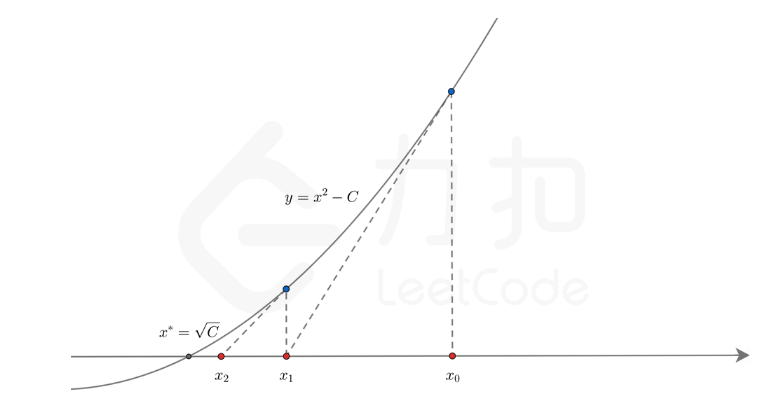


代码示例:(Java)
public class Solution3 {
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (Math.abs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return (int) x0;
}
}
复杂度分析
- 时间复杂度:O(logx),此方法是二次收敛的,相较于二分查找更快。
- 空间复杂度:O(1)。
考察知识点
收获
1.二分查找
2.牛顿迭代

