题目出处
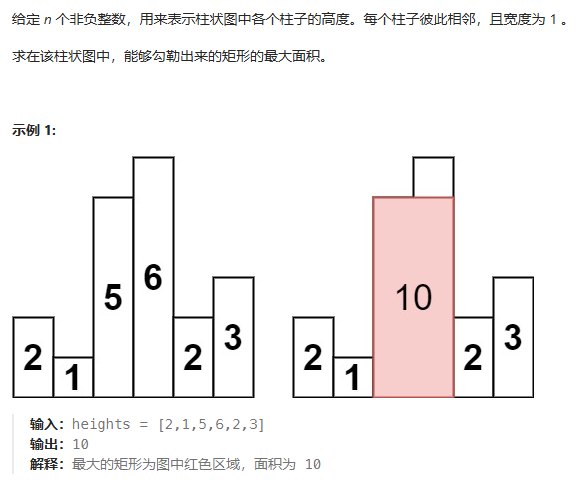
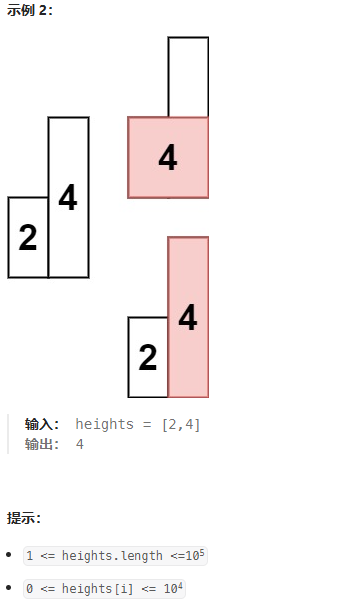
题目描述
个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
前言

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
int ans = 0;
// 枚举左边界
for (int left = 0; left < n; ++left) {
int minHeight = INT_MAX;
// 枚举右边界
for (int right = left; right < n; ++right) {
// 确定高度
minHeight = min(minHeight, heights[right]);
// 计算面积
ans = max(ans, (right - left + 1) * minHeight);
}
}
return ans;
}
};

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
int ans = 0;
for (int mid = 0; mid < n; ++mid) {
// 枚举高
int height = heights[mid];
int left = mid, right = mid;
// 确定左右边界
while (left - 1 >= 0 && heights[left - 1] >= height) {
--left;
}
while (right + 1 < n && heights[right + 1] >= height) {
++right;
}
// 计算面积
ans = max(ans, (right - left + 1) * height);
}
return ans;
}
};

方法1:单调栈
思路:



代码示例:(Java)
public class Solution1 {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] left = new int[n];
int[] right = new int[n];
Deque<Integer> mono_stack = new ArrayDeque<Integer>();
for (int i = 0; i < n; ++i) {
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
mono_stack.pop();
}
left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
mono_stack.push(i);
}
mono_stack.clear();
for (int i = n - 1; i >= 0; --i) {
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
mono_stack.pop();
}
right[i] = (mono_stack.isEmpty() ? n : mono_stack.peek());
mono_stack.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(N)。
- 空间复杂度:O(N)。
方法2:单调栈 + 常数优化
思路:

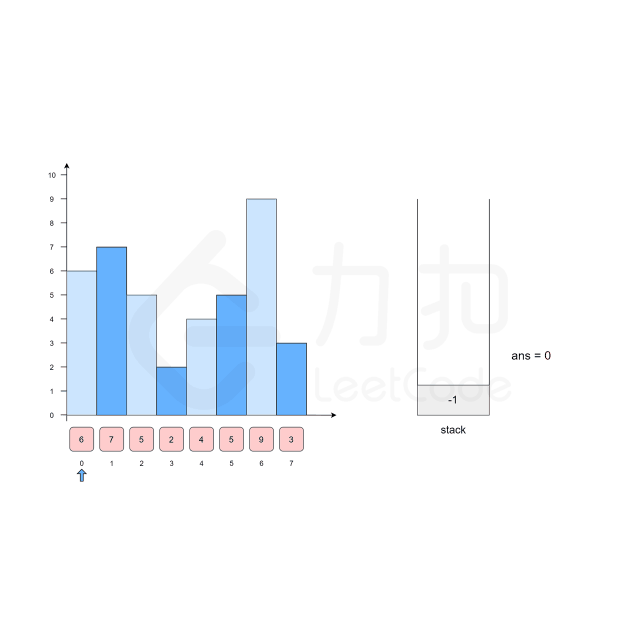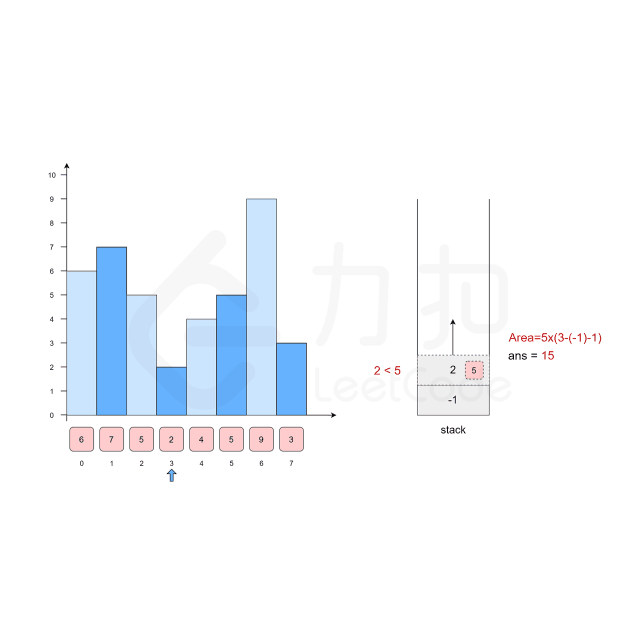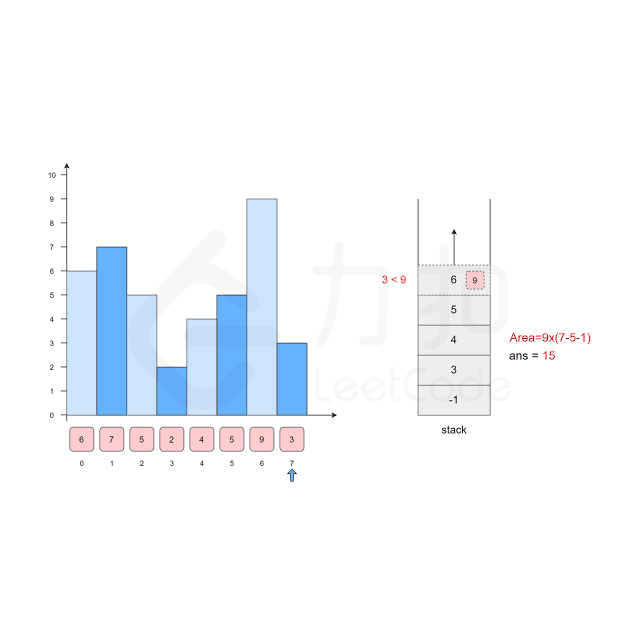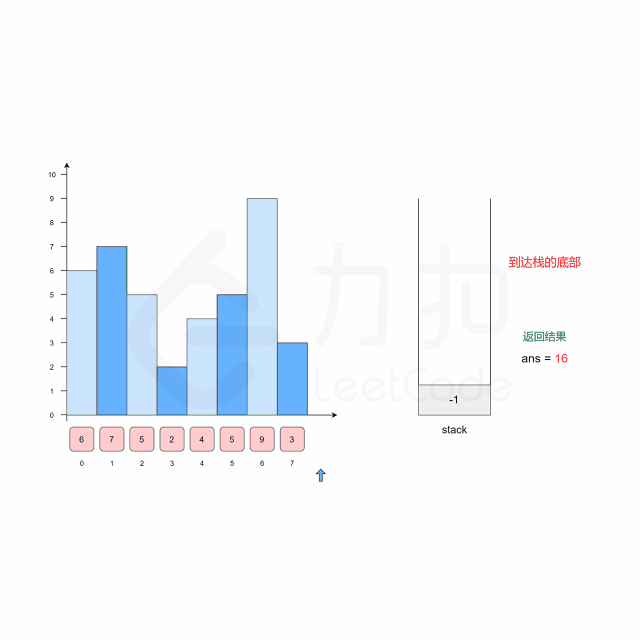
代码示例:(Java)
public class Solution2 {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] left = new int[n];
int[] right = new int[n];
Arrays.fill(right, n);
Deque<Integer> mono_stack = new ArrayDeque<Integer>();
for (int i = 0; i < n; ++i) {
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
right[mono_stack.peek()] = i;
mono_stack.pop();
}
left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
mono_stack.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(N)。
- 空间复杂度:O(N)。

