题目出处
题目描述

个人解法
思路:
todo
代码示例:(Java)
todo
复杂度分析
todo
官方解法
方法1:使用柱状图的优化暴力方法
思路:

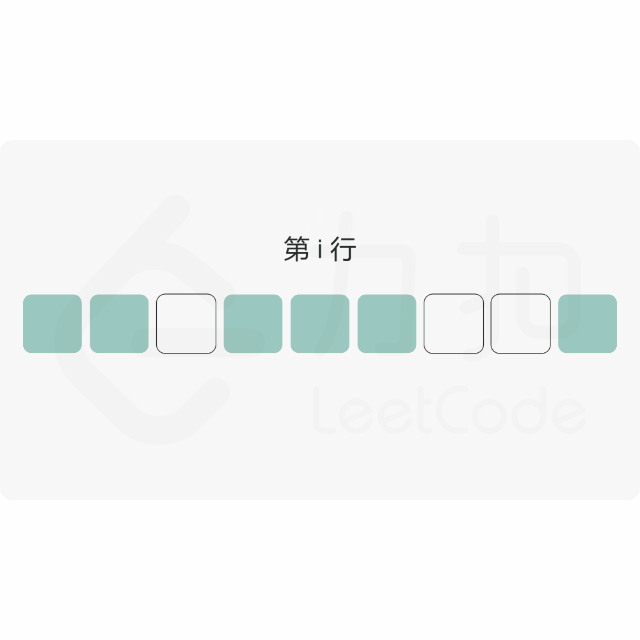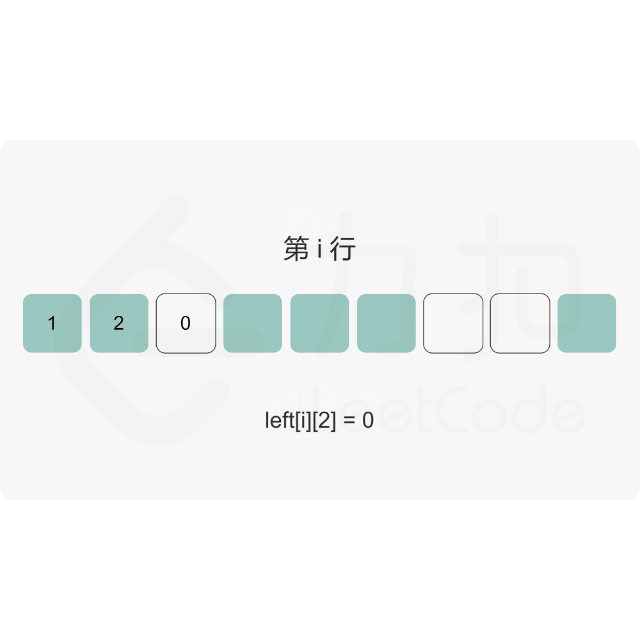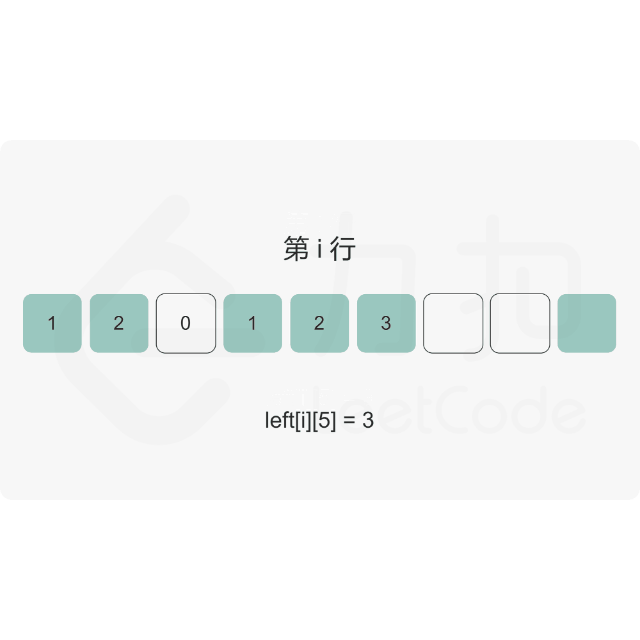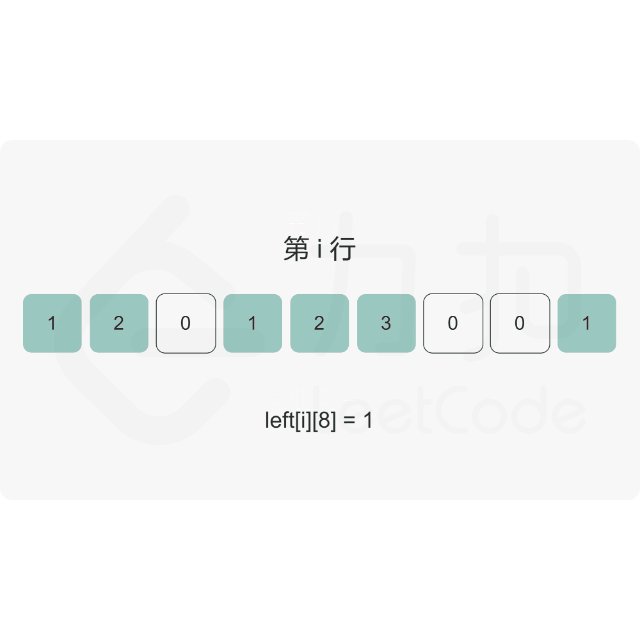

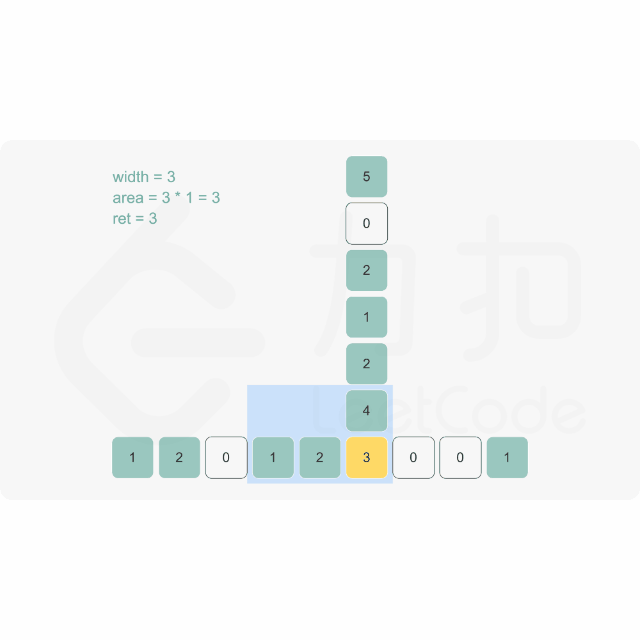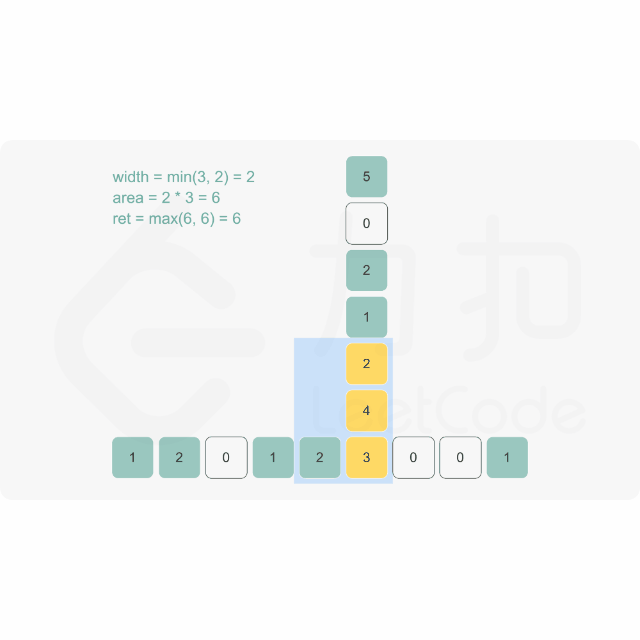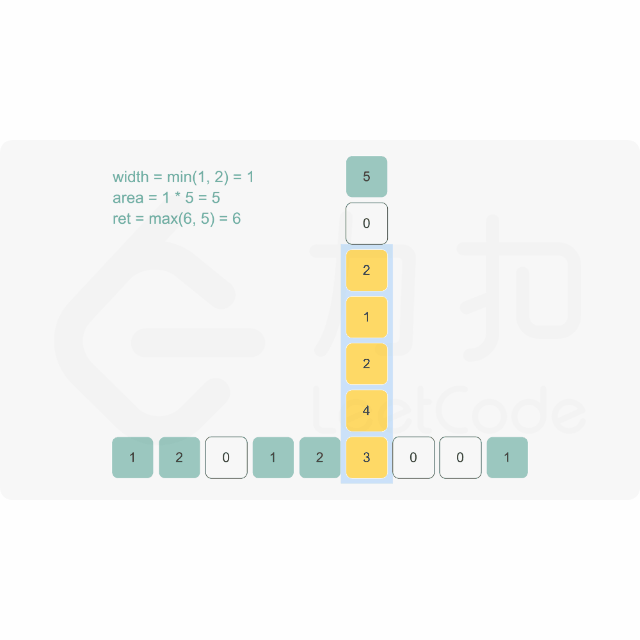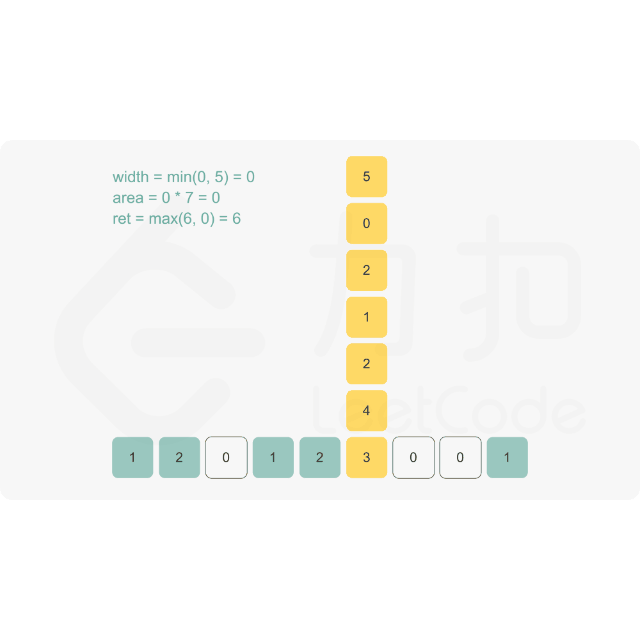

代码示例:(Java)
public class Solution1 {
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
if (m == 0) {
return 0;
}
int n = matrix[0].length;
int[][] left = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
}
}
}
int ret = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '0') {
continue;
}
int width = left[i][j];
int area = width;
for (int k = i - 1; k >= 0; k--) {
width = Math.min(width, left[k][j]);
area = Math.max(area, (i - k + 1) * width);
}
ret = Math.max(ret, area);
}
}
return ret;
}
}
复杂度分析

方法2:单调栈
思路:

代码示例:(Java)
public class Solution2 {
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
if (m == 0) {
return 0;
}
int n = matrix[0].length;
int[][] left = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
}
}
}
int ret = 0;
for (int j = 0; j < n; j++) { // 对于每一列,使用基于柱状图的方法
int[] up = new int[m];
int[] down = new int[m];
Deque<Integer> stack = new LinkedList<Integer>();
for (int i = 0; i < m; i++) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop();
}
up[i] = stack.isEmpty() ? -1 : stack.peek();
stack.push(i);
}
stack.clear();
for (int i = m - 1; i >= 0; i--) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop();
}
down[i] = stack.isEmpty() ? m : stack.peek();
stack.push(i);
}
for (int i = 0; i < m; i++) {
int height = down[i] - up[i] - 1;
int area = height * left[i][j];
ret = Math.max(ret, area);
}
}
return ret;
}
}
复杂度分析


